🤖 모델 적합도(Model Fit)와 편향(Bias) · 분산(Variance)

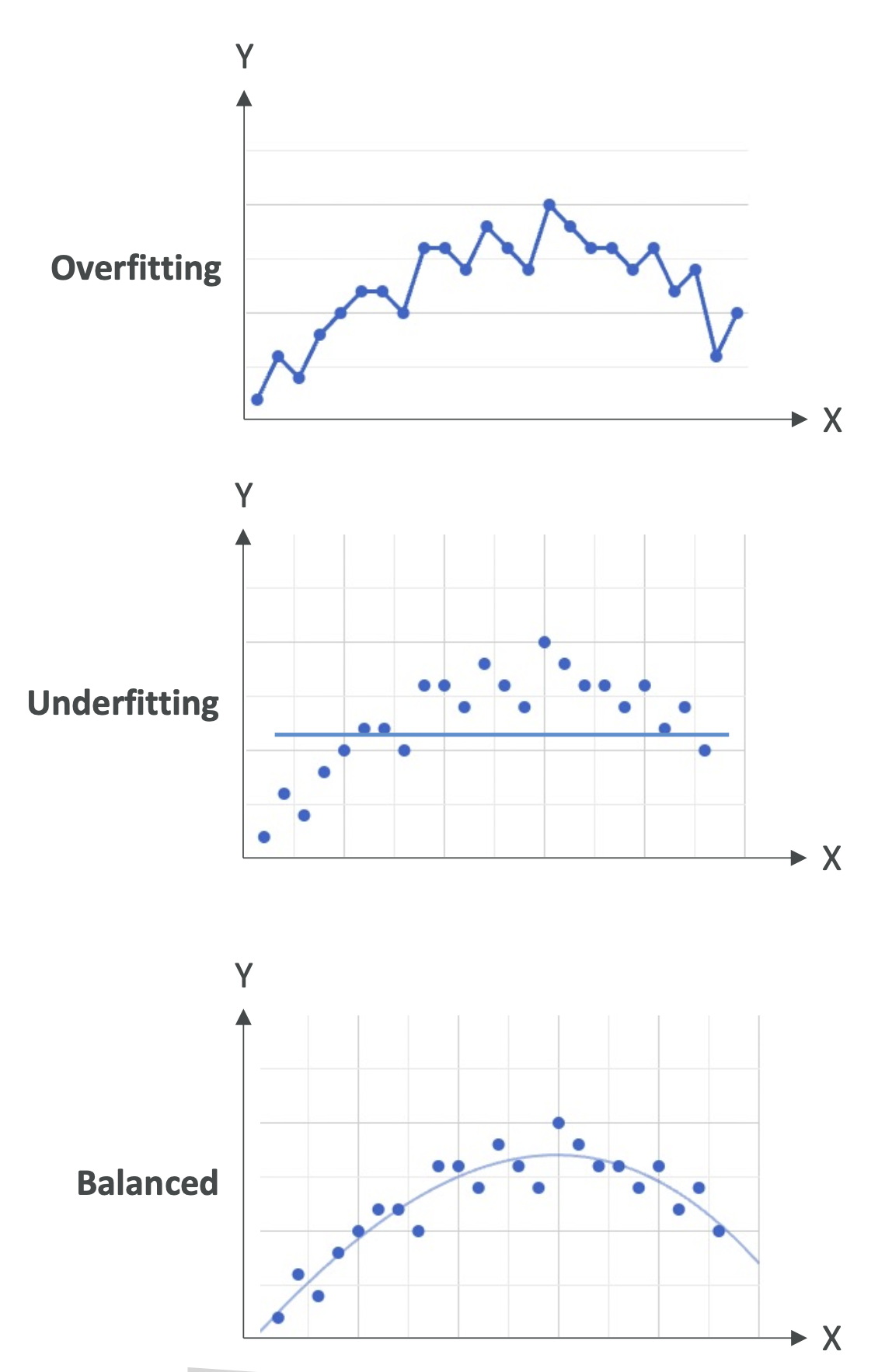
1. 모델 적합도(Model Fit)

머신러닝 모델이 제대로 동작하지 않을 때는 모델의 적합도(Fit) 를 살펴봐야 합니다.
모델이 데이터를 얼마나 잘 설명하는지가 핵심입니다.

• 과적합(Overfitting)
• 훈련 데이터에서는 성능이 매우 좋음
• 새로운 데이터(검증/테스트 데이터)에서는 성능이 나쁨
• 원인: 모델이 데이터의 노이즈까지 학습해서 일반화가 안 됨
• 📌 예시: 훈련 데이터 점 하나하나에 맞게 선을 구부려 만든 복잡한 곡선
• 과소적합(Underfitting)
• 훈련 데이터에서도 성능이 나쁨
• 원인: 모델이 너무 단순하거나, 특징(Feature)이 부족함
• 📌 예시: 복잡한 곡선 데이터에 단순 직선을 억지로 적용
• 균형(Balanced)
• 과적합도, 과소적합도 아닌 상태
• 어느 정도 오차는 있지만, 데이터의 전체적인 패턴을 잘 따름
• 📌 가장 이상적인 상황

---

2. 편향(Bias)과 분산(Variance)

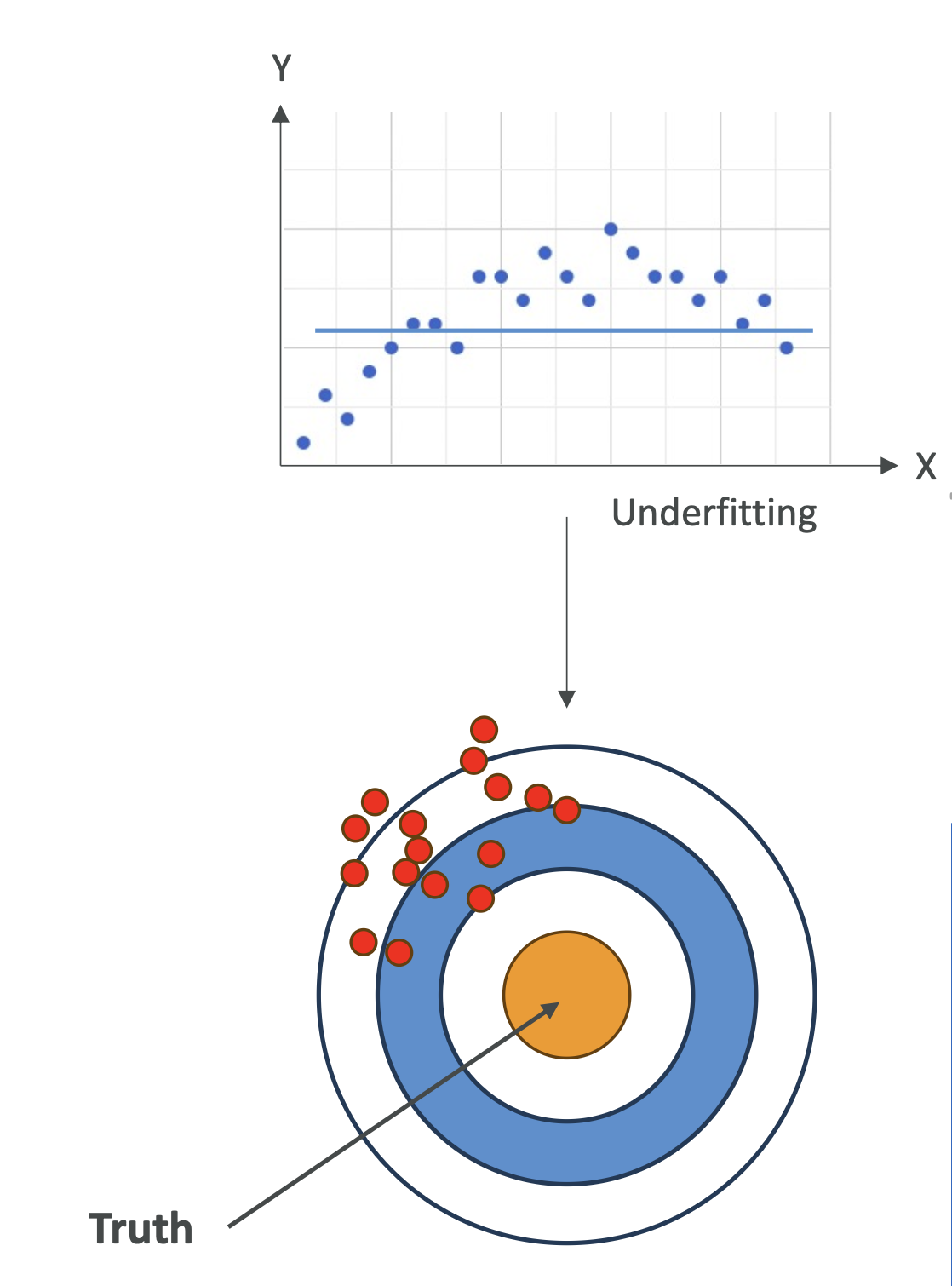
📌 Bias (편향)

• 정의: 실제 값과 예측 값의 차이
• High Bias (편향 높음)
• 모델이 데이터 패턴을 잘 잡지 못함 → 과소적합
• 예시: 곡선 패턴 데이터를 직선으로 예측
• 줄이는 방법
• 더 복잡한 모델 사용 (예: 선형 → 비선형 모델)
• 더 많은 특징(Feature) 추가

---

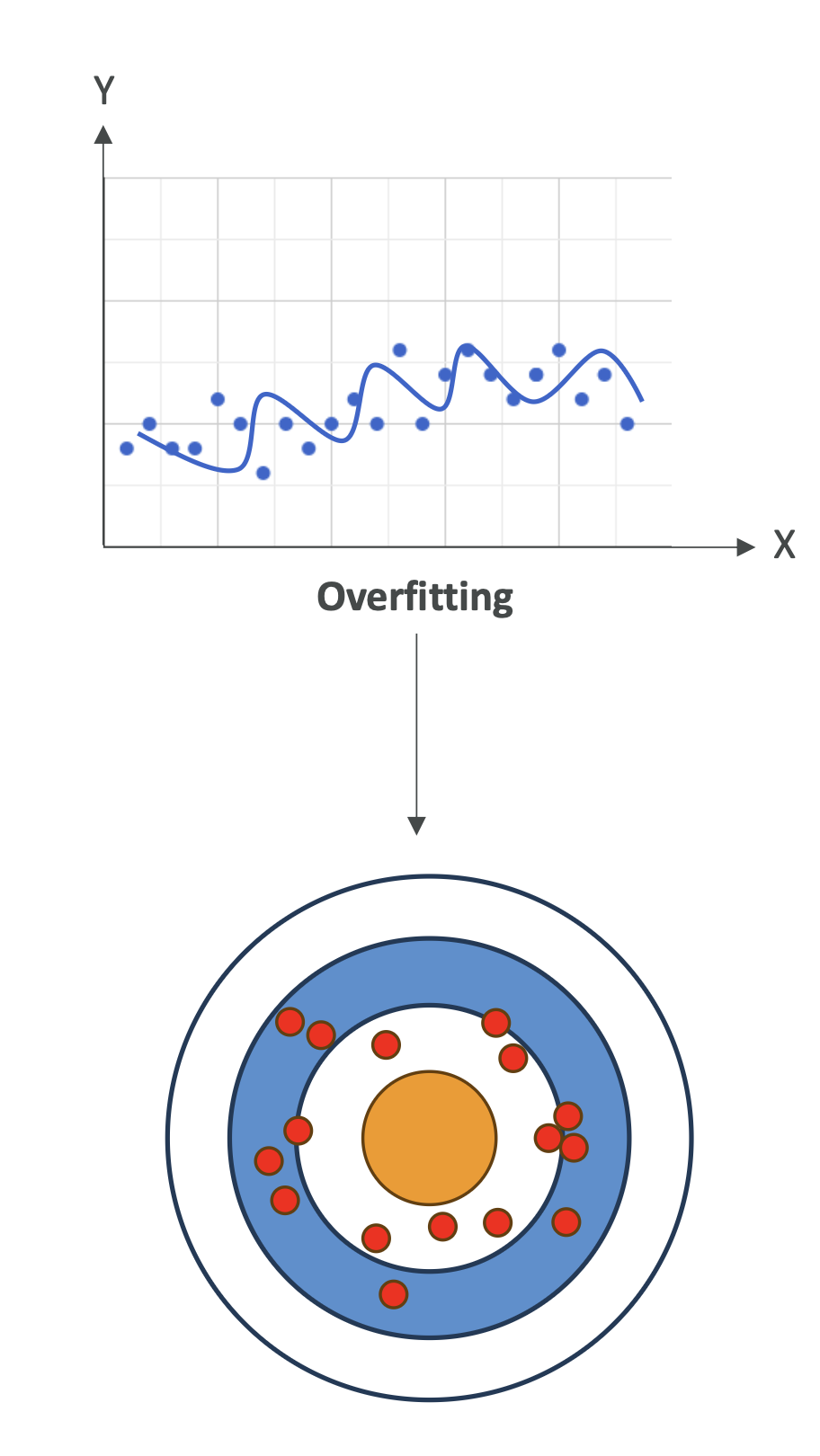
📌 Variance (분산)

• 정의: 훈련 데이터를 조금만 바꿔도 모델 성능이 크게 달라지는 정도
• High Variance (분산 높음)
• 훈련 데이터에서는 성능이 매우 좋지만, 새로운 데이터에서는 성능이 급격히 떨어짐
• 즉, 과적합 상황
• 줄이는 방법
• 불필요한 특징 제거 (Feature Selection)
• 데이터셋을 여러 번 나눠서 교차검증(Cross Validation) 수행
• 정규화(Regularization, 예: L1/L2) 적용

---

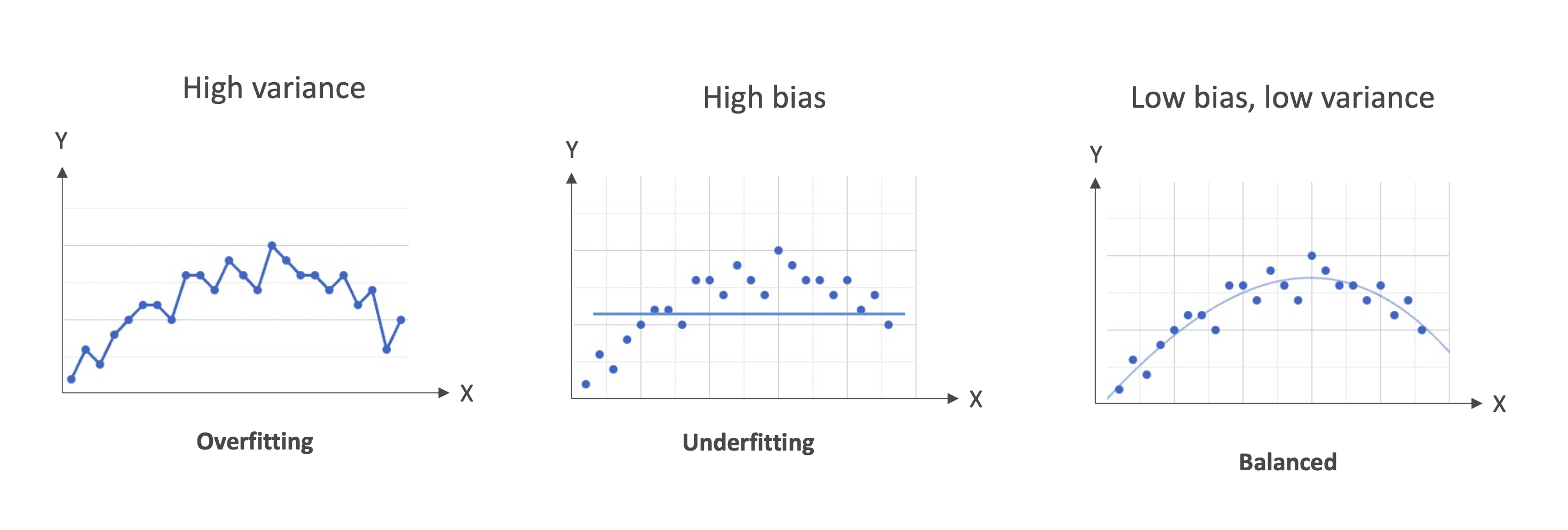
3. Bias-Variance Tradeoff (편향-분산 트레이드오프)

머신러닝에서는 Bias(편향) 과 Variance(분산) 사이에서 균형을 맞추는 것이 중요합니다.

• High Bias + Low Variance → 과소적합
• Low Bias + High Variance → 과적합
• Low Bias + Low Variance → 이상적인 모델
• High Bias + High Variance → 최악의 경우 (피해야 함)

📌 시험 포인트:

• 과적합 ↔ 분산 높음 (Variance High)
• 과소적합 ↔ 편향 높음 (Bias High)
• 균형 잡힌 모델이 가장 좋은 상태

---

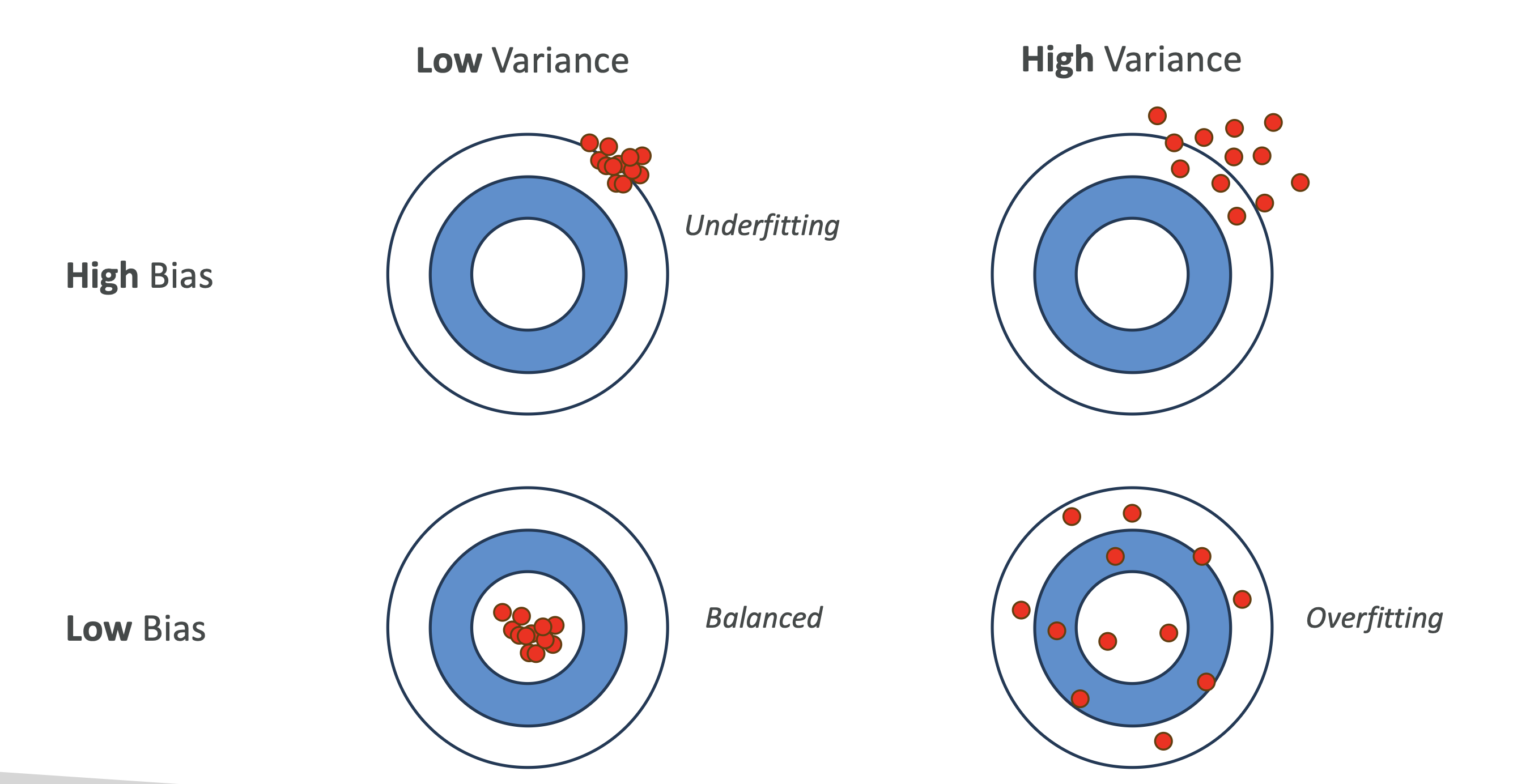
4. 시각적 이해 (다트판 예시 🎯)

• 편향(Bias): 다트가 과녁의 중심에서 얼마나 떨어져 있는지
• 분산(Variance): 다트가 흩어져 있는 정도

구분	설명	결과
High Bias + Low Variance	계속 같은 위치에 맞추지만 중심에서 멂	Underfitting
Low Bias + High Variance	중심 근처에 맞추지만 흩어져 있음	Overfitting
Low Bias + Low Variance	중심에 가깝고 모여 있음	Best Model
High Bias + High Variance	멀리 있고 흩어져 있음	Worst Model

---

✅ 시험 대비 Key Takeaways

1. Overfitting → 훈련 데이터 잘 맞춤, 테스트 데이터 성능 나쁨 → Variance ↑
2. Underfitting → 훈련 데이터조차 성능 나쁨 → Bias ↑
3. Balanced Fit → Bias와 Variance 모두 낮아야 함
4. Bias-Variance Tradeoff 개념 숙지 필수
5. AWS 자격증 시험에서는 과적합 / 과소적합을 어떻게 해결할지를 물을 수 있음

• 과적합 해결: Regularization, Feature Selection, Cross Validation
• 과소적합 해결: 더 복잡한 모델, Feature 추가